The first paper that describes some of the functionality of psychonetrics has now been published open access in Psychometrika, with all code available at the Open Science Framework. In this paper, I discuss estimation of latent network models from time-series and panel data. Such latent-variable models can always be written as an observed variable models, so all discussed models can also be used as ‘regular’ network models for observed data only. As such, the paper also introduces new estimation methods for the popular graphical vector-autoregression (GVAR) model through non-regularized estimation from either time-series or panel data. In addition to the published paper, new teaching materials are now also available online in our winter school materials (see day 3, part 2). In this blog post I summarize some key points from the paper.
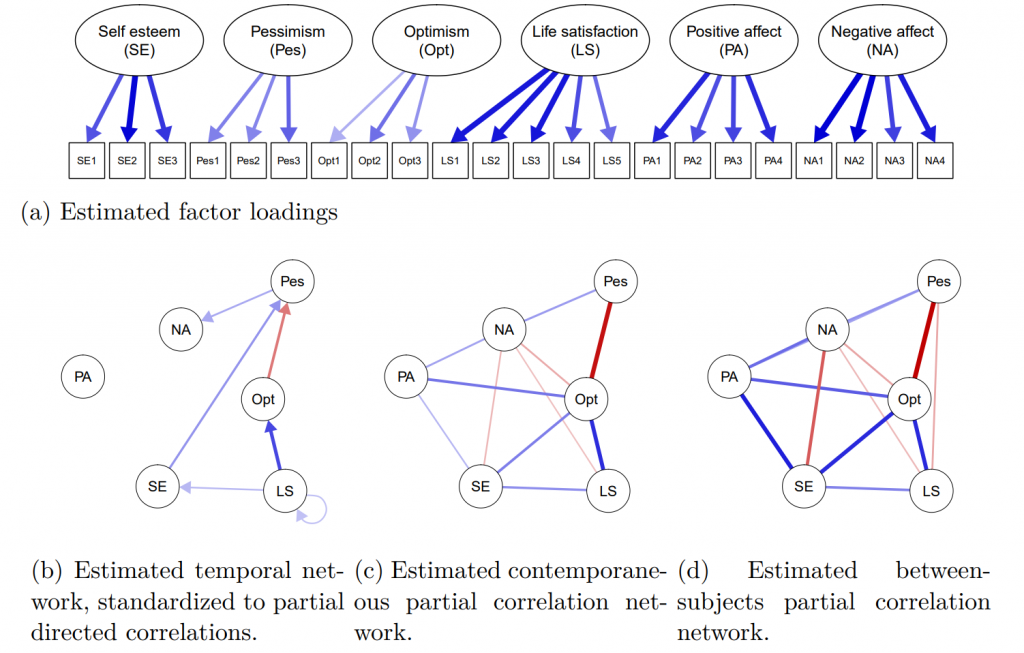
Implementation in psychonetrics. The panel data model has been implemented in psychonetrics through the dlvm1 function, and the time-series model has been implemented through the tsdlvm1 function. Some convenient wrappers are: panelgvar for specifying a GVAR model on panel data, gvar for specifying a GVAR model on time-series data, and ml_ts_lvgvar for specifying a panelgvar model using the same input as the mlVAR package.
Networks from panel data. One of the main contributions of this paper is that it introduces network estimation from panel data. This fills an important gap in network psychometrics: many models and estimation methods now exist for cross-sectional data and intensive time-series data, but not many models yet existed for panel data designs. When using only observed variables in the network, the panel data model takes the form of a random intercept cross-lagged panel model, except that the contemporaneous and between-subjects structures are modeled as networks. This allows for the same fixed-effects decomposition as used in my earlier work on time-series modeling: temporal, contemporaneous, and between-subjects networks can be obtained. Of note, when full-information maximum likelihood (FIML) estimation is used, the panel data model is a multi-level GVAR model (as implemented in mlVAR) with only random intercepts (no random network parameters). To this end, the panel data model allows for estimating multi-level GVAR models on datasets where only a few observations are available per person. This opens the door to some new types of research. For example, when the interest is only to obtain fixed-effects networks, an alternative to gathering intensive time-series per person is simply to gather only a few observations of many people. In addition, the lag interval can drastically be increased in such settings by modeling lag intervals of, say, a year in panel data designs (although it may not be expected that temporal effects are very strong in such designs).
Model search algorithm. In the paper, I introduce the new modelsearch algorithm that has been implemented in the last version of psychonetrics. This algorithm is a variant of the ggmModSelect algorithm that is now often used when estimating Gaussian network models, but utilizes significance values and modification indices to reduce the model search space:
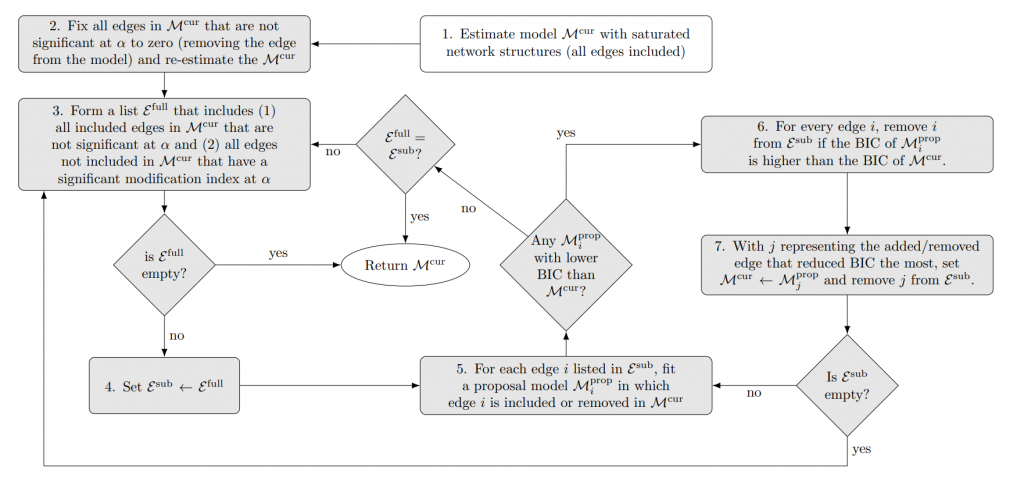
The algorithm can be used for any single-group model in psychonetrics that is estimated through maximum likelihood estimation. Simulations in the paper show good performance of this method in retrieving the underlying network structure from time-series and panel data.
Ergodicity and Generalizability. Pages 20 and 21 of the paper extensively discuss my thoughts on within- versus between-subject interpretations. I show that ergodicity holds only under complete homogeneity of intercept and network structures (factor loading structures are already assumed invariant across people and levels), and that a complete within-person interpretation of the panel data networks only hold under homogeneity of network structures (otherwise, the interpretation is that of a fixed-effects model). However, I also discuss that these terms are not optimal. ‘Within-person’ and ‘between-person’ terms purely relate to mathematical aspects of the modeling framework (a part that is stable and a part that deviates from this), and it is entirely possible that between-person relations are within-person relations on a different time-scale. In fact, in aging and developing humans with a fixed life-span, only very few aspects can truly be considered within-person. In order to find generalizable results across populations, we will likely require to analyze various sources of data, including valuable cross-sectional and panel data designs with many subjects.
The winter school materials include an example of this point. Suppose we are interested in the following relationship in a hypothetical person measured over time:
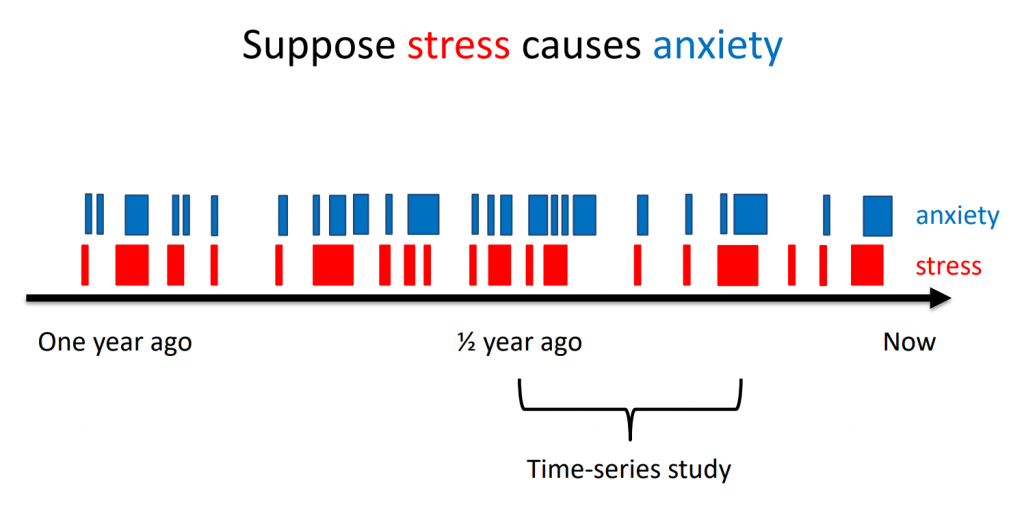
Here, a red block indicates the person experiences stress, and a blue block indicates the person experiences anxiety. Most bouts of anxiety trigger shortly after stress starts. As a result, we may be able to find a within-person relationship between stress and anxiety in our time-series study. Even better, this relationship may even be captured in the temporal network if we choose our lag-interval correctly. Now suppose, however, we are interested in the following relationship:
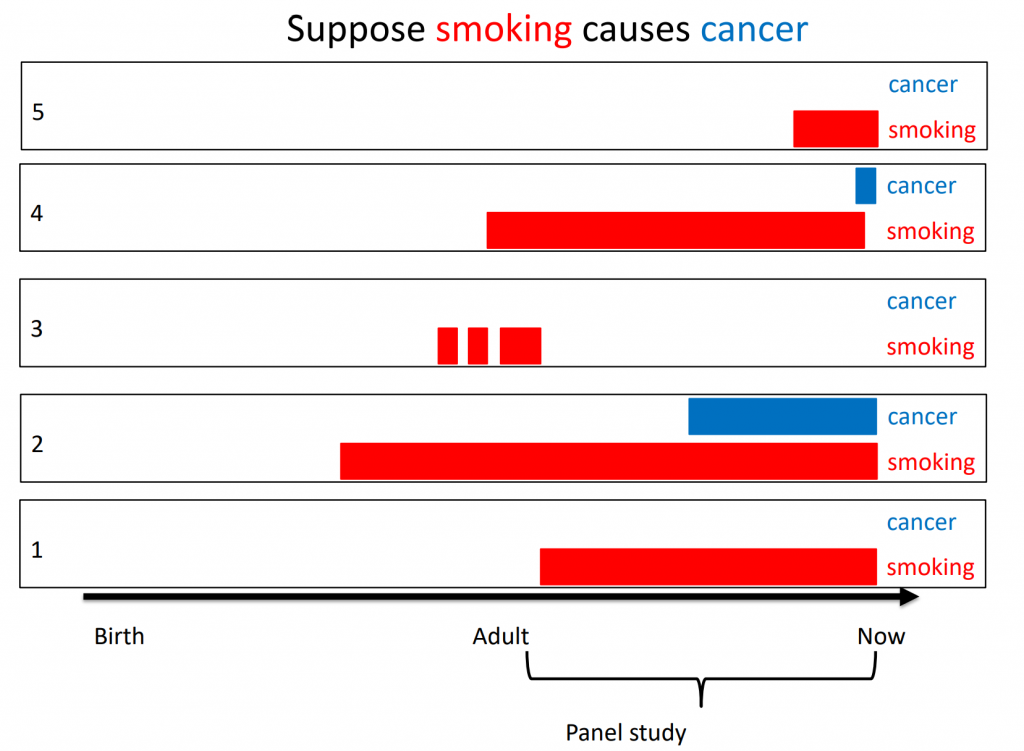
In this case, we cannot possibly hope to find within-person relationships following any person over time in a short window of analysis (e.g., weeks to months as in the example above). Comparing people at any time-point, however, may lead to insightful relationships. In a lengthy panel-design setup we may also be able to find within-person relationships in the fixed-effects structure, and these may even be included in the temporal network. To this end, between-person relationships at one time-scale may very well be within-person relationships at another time-scale.
Conclusion. I conclude the paper with an overview of limitations, related work, and future directions. In particular, assumptions underlying the modeling framework (e.g., stationary and normality) may be problematic in practice, and the modeling framework is closely related to various other modeling techniques (e.g., dynamical factor models, latent/residual network models for cross-sectional data, and cross-lagged panel models). Some important future directions will be to assess additional functionality already implemented in psychonetrics. Notably,
residual network modeling modeling and multi-group designs are also possible for time-series and panel data designs, and should be investigated in more detail in future work.
Recent Comments