About twenty years ago, I was a young teenager when my two-year older brother introduced me to the increasingly popular card game Magic the Gathering (MTG). We both liked the game a lot and started to collect cards, making sure that all the blue cards would go to my brother and all the black cards would go to me. Back then, my main goal in life was to defeat my brother, a.k.a. the eternal rival, in any game we played. I failed at this goal in pretty much every game, and MTG was no exception. My brother won game after game after game.
But then there was a turning point. A MTG shop opened in our hometown of Blaricum, which started to host tournaments as well with about twenty people participating. I won the first five tournaments they hosted. In some of them, the finale would be between me and my brother. They were tense games, but I won. After reigning as undisputed champion of Blaricum for about a year, I retired from playing MTG tournaments, thus never to be beaten since in any semi-official setting (my brother would go on to become a professional MTG player and subsequently a professional poker player, playing tournaments of both games at the highest levels worldwide).

Me and my brother: two teenage wizards in the middle of a fierce battle of wits and randomness. Note that the bunny referee is not effective as (a) the flowers obstructs the view to the arena, and (b) it is a plushie bunny who has not been educated in the game.
Stacking the deck in my favor
How did I win five consecutive tournaments while statistically I should have lost some times to my brother, a far better MTG player before and after these tournaments? In retrospect, I doubt that my victories were entirely fair. To simplify MTG, each player has their own deck of 60 cards, which consists of 20 lands and 40 spells (for me at least, other players chose different distributions of lands and spells). You start the game by drawing the top 7 cards from your deck, and subsequently draw one more card each turn. Each turn, you can only play one land card, which you use to pay for spells. A crucial aspect of MTG is that you want to start your game with about 2 to 3 lands in your hand. Less, and you are too likely to run dry, not being able to pay for your spells. More, and you don’t have enough spells to play which will surely make you lose the game.
Ideally you start the game with a completely randomized deck, which is done by shuffling your deck. There are many shuffling techniques; I only really knew how to perform the most common one, the overhand shuffle. The overhand shuffle is performed as follows: you take the deck in one hand, throw a pack of consecutive cards from the top to your other hand (retaining the order of cards in the pack), throwing a second pack of consecutive cards from the top to your other hand (landing on the first pack), etcetera. In practice, it means that you separate your deck in a number of packs of roughly equal size, and subsequently re-stack them in reversed order. Finally, the whole process is repeated several times (the more times the process is repeated the more random the shuffle).
Teenage me learned to employ a certain, questionable, strategy when shuffling my deck: rather than collecting my cards at random, I would quickly re-arrange the lands such that they were equally spread throughout the deck: land, spell, spell, land, spell, spell, etcetera (I would do the same for some combo cards, but will simplify this post to only discuss lands). Thus, I literally stacked the deck in my favor. Next, I would shuffle the deck using the overhand shuffle, but would make sure I did not separate my deck in too many packs (say, three to five packs), and did not repeat the process too many times (say, three times). Why is this strategy questionable? Well, let’s study its effect in R!
Investigating shuffling techniques
First we can load some helper functions (available online here), and set the random seed:
source("magicFuns.R")
set.seed(100)
Now, we can construct a dummy MTG deck, with 60 cards, 20 of which are lands that are evenly spread out over the deck:
deck <- createDeck()
plotDeck(deck)
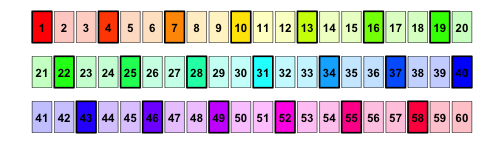
An unshuffled deck: highlighted cards represent “lands” and other cards represent “spells”. The first seven cards (reading from top left) form the “starting hand”.
The highlighted cards represent lands, and the color and number on each card represent the position of the card in the original order. In this beautifully unshuffled deck, I would start with 3 lands in my 7-card opening hand.
Now let’s see what happens if I shuffle the deck. The overhand function mimics the overhand shuffle, it divides the deck in three to five packs of roughly equal size, then re-stacks the deck by reversing the order of the packs. Suppose I apply three overhand shuffles:
deck_shuffled <- deck %>%
overhand %>%
overhand %>%
overhand
plotDeck(deck_shuffled)
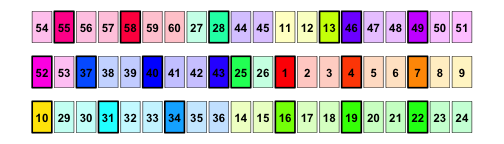
Example of a deck after an overhand shuffle with three to five packs, repeated three times.
What do we now see? Sure, the deck is somewhat randomized, but large consecutive blocks of cards remain consecutive, and all the lands remain spread out over the deck. In this case, I would even start my hand with 7 consecutive cards from the original order (54 to 60)! This includes two lands (perfect!), but could even include a nice distribution of spells if I stacked spells too to be spread out over the deck (e.g., no two identical spells next to each other). Let’s compare this to what a properly shuffled deck looks like:
deck_shuffled2 <- deck %>% properShuffle
plotDeck(deck_shuffled2)
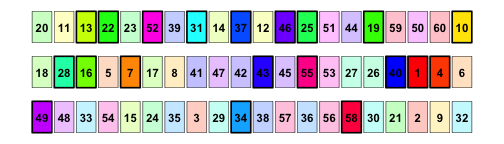
Example of a deck that is properly shuffled.
Now, I would start with 3 lands, but would draw more lands than I would like in the next turns. The last 20 cards would only contain 3 lands, and it would completely ruin my game if those were the first 20 cards.
But these are just two examples. Let’s perform a quick simulation study to check these shuffling strategies, repeating the above 1,000 times:
# Overhand simulation:
sim_overhand <- replicate(1000, {
deck_shuffled <- deck %>% overhand %>% overhand %>% overhand
sum(deck_shuffled$type[1:7] == "land")
})
# Proper simulation:
sim_proper <- replicate(1000, {
deck_shuffled <- deck %>% properShuffle
sum(deck_shuffled$type[1:7] == "land")
})
# Combine in data frame:
df <- rbind(
data.frame(type = "overhand", nLand = sim_overhand),
data.frame(type = "proper", nLand = sim_proper)
)
# Plot:
library("ggplot2")
ggplot(df, aes(x=factor(nLand))) +
geom_bar() +
facet_grid(type ~ .) +
xlab("Number of lands in starting hand") +
ylab("Number of hands")
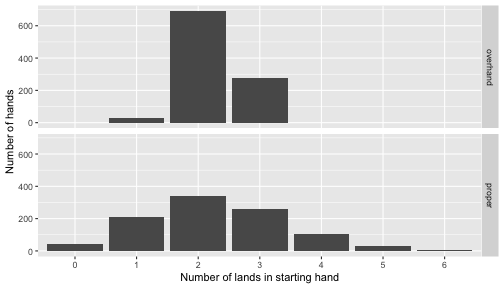
Distribution of number of “land” cards in the starting hand after using my variant of the overhand shuffle and proper shuffling techniques.
This tells us that with my shuffling technique, I am virtually guaranteed to start with 2 to 3 lands, while proper shuffling would add much more randomness. Therefore, my shuffling technique gave me a massive edge over a player who would properly shuffle his or her deck (e.g., my brother, who actually knew how to shuffle a deck as well as proper tournament regulations).
Why did I use questionable Magic practices?
Thinking back on why I employed these questionable practices, I don’t recall myself as a 15-year old boy cheating to win some tournaments. However, I also don’t recall myself being completely oblivious to the effects of my shuffling technique. I knew my shuffling technique would lead to more consistency, but I fully believed I played and won these tournaments fairly. Why? I can think of some reasons:
- I thought I was acting in an acceptable range of the norm — The overhand shuffle was the shuffling technique everyone else used, and was the only real shuffling technique I could perform. I saw it as the way cards are supposed to be shuffled. This means also that not using the overhand shuffle would cripple my performance. The questionable aspects — stacking my deck before shuffling, using only three to five packs and repeating only three times — did not seem to me to lie outside an acceptable range of what everyone else was doing.
- I knew how my deck was supposed to work — It was very carefully constructed with all kinds of interesting combo cards designed to set up powerful plays of counter certain moves. I knew I should start with two or three lands in my opening hand, as that is how I designed the deck. I did not want some random chance, such as starting without lands, to ruin my game when it mattered the most: in the finale of the then most important tournament of my life against my brother.
- I did not fully grasp what proper randomness should look like — I always played using this shuffling technique, and therefore I saw nothing wrong with the performance of my deck during the tournaments; it performed as it was supposed to. Every time my opponent was smart enough to request to shuffle the deck more, though, I felt like I had a lower chance of winning. So much, that I actually saw this as a questionable practice my opponent used on me: using a shuffling technique that deliberately destroyed the performance of my deck.
From questionable Magic practices to questionable research practices
Why am I suddenly confessing the use of questionable Magic practices two decades ago? Should my five victories be scrapped from the record? Possibly, but I doubt that hardly anyone even remembers them. Should I accept that I am not a masterful MTG player? Probably, but had I continued a career in MTG that would likely soon have been rectified in numerous failed replications in better and more controlled settings.
No, this story is actually not at all about questionable Magic practices, but rather about questionable research practices (QRPs): practices that are not necessarily fraudulent, but that may increase the probability of obtaining a significant finding (increasing the type 1 error rate). QRPs may include, among other things, gathering more data after finding a non-significant result, arbitrary removal of data (outliers), selective reporting of results, ad-hoc hypothesizing and rounding p-values in your favor.
To combat QRPs, we need to understand why people use QRPs. Too often, I see the use of QRPs heavily condemned and the researchers that use them almost painted as fraudsters. However, I believe that researchers that employ QRPs do not do so with bad intentions. My story of winning MTG by stacking the deck in my favor easily translates to possible reasons why researchers employ QRPs:
- Researchers think they are acting in an acceptable range of the norm — Likely, many researchers are just acting in the way they think is best and the way they have been taught. Many QRPs are simply routine practice in research, and may even be taught during courses or thesis supervision. Everyone else seems to be selective in reporting results, removing outliers after already performing the analysis, and adapting the introduction and hypotheses after studying the results when writing the final product — why can’t I?
- Researchers may think they ‘know’ how a theory is supposed to perform — A researcher may, with the best of intentions, fully believe in the theory that is being studied and its benefits to society if it is correct. To this end, the researcher may make some slight adjustments to the results (e.g., remove an outlier) because the researcher may truly believe the original results are ‘wrong’. The theory is also supported by research from esteemed professor X, described in textbook Y, and is the basis of a million plus euro grant funding not only me but my professor and several colleauge/friend postdocs/PhDs, who are all getting significant results. The theory cannot be wrong, so surely the data is wrong!
- Researchers may not fully grasp what proper randomness should look like — Perhaps the most worrisome of all. True randomness is awefull and ugly. A histogram based on a true random sample from a normal distribution may look not bell-shaped at all, under a true null one in twenty results may give a significant result, the sampling error around point estimates may be huge, etcetera. Studying a weak effect may lead to a large type 2 error rate (low power), especially when the sample size is based on prior research affected by publication bias. This means that even when an effect is real, there is a sizable chance of finding a non-significant effect. For science, this is a good thing — ideally we would replicate anything dozens of time and then see how well something performs. But for an individual researcher this may be terrible: a year spent investigating something during a PhD may lead to a finding not at all congruent with other literature, making it seem the researcher did something wrong perhaps. I was ok with losing MTG to my brother again and again, but did not want to lose to random chance when it mattered most: in the finale of the most important tournament of my life. PhD-students and early career researchers especially are always playing the most important tournament fo their life.
I think these are all fair reasons from a personal level, and make it clear that for a large part the individual researchers — who likely try their best to perform their research as honest and thorough as they can, ultimately hopefully helping society in general with their findings — are not the ones to blame and should not be condemned as fraudsters.
Solving questionable magic and research practices
So how to solve the issues described in this blog post? To me, the answers seem rather straightforward:
- Education — Educating an MTG player on how to properly shuffle a deck and what randomness looks like would help preventing questionable Magic practices. Likewise, educating researchers on good research practices and the dangers of QRPs would help prevent QRPs. Our research master program at the University of Amsterdam has an entire course dedicated to this, as well as guidelines throughout the master (e.g., the thesis must have a confirmatory and exploratory analyses section). Thanks to these efforts in education, our master students are amazing at open science practices. For example, during my last course on factor analysis, I let students preregister (sending me a report) an expected factor model in weeks 1 and 2, let them gather data in week 3, and analyze the data in week 4. I also teach measurement invariance in week 3, and told students they could do it on their gathered data as well if they like (these projects were all fun projects intended to practice not to publish anyway). I had several students ask me if it would be ok to also perform measurement invariance tests, even though they had not pre-registered these analyses.
- Changing the norms — Educating researchers is a start, but to really combat QRPs we need to take away the incentives to use QRPs. For a teenager playing MTG, perhaps a year-long league would be better than a single match to decide who is the best MTG player in Blaricum. For a researcher, results should not impact the importance of a study and its consequences for the future career of the researcher. This can be accomplished by preventing publication bias, results blind reviewing, and a more general acceptance towards also finding non-consistent results. If a PhD student studies the same phenomena five times with a power of 0.80, then it should be expected one paper will report a non-significant result. As with the land distribution above, this means that finding two or even three non-significant results is also fully in the range of possibilities. And this should be ok. Other ways in which the norms can be changed is by making better research practices readily available to researchers, such as is done by the great JASP team.
- External checks — In a proper MTG tournament, a player cannot do what I did. There are officially licensed referees as well as other players who know the rules. When they see you shuffle the deck (which you have to do above the table in the open), they may complain about the method used or even disqualify you from a tournament. Likewise, in science there should also be external checks. Tools such as Michèle Nuijten’s statcheck help in this, but the best advances come in the form of open science and through platforms such as the open science framework. Like an MTG player has to shuffle the deck above the table, a researcher should also make it clear how, exactly, the analyses were performed, preferably with the data.
I believe that the field of psychological research is making great progress in these solutions already, and look forward to a future of good practices in psychological research and local MTG tournaments.